This page presents a brief summary of some research and projects I have done to date, starting with newer work at the top.
Active Generation - Generative models for black box optimisation
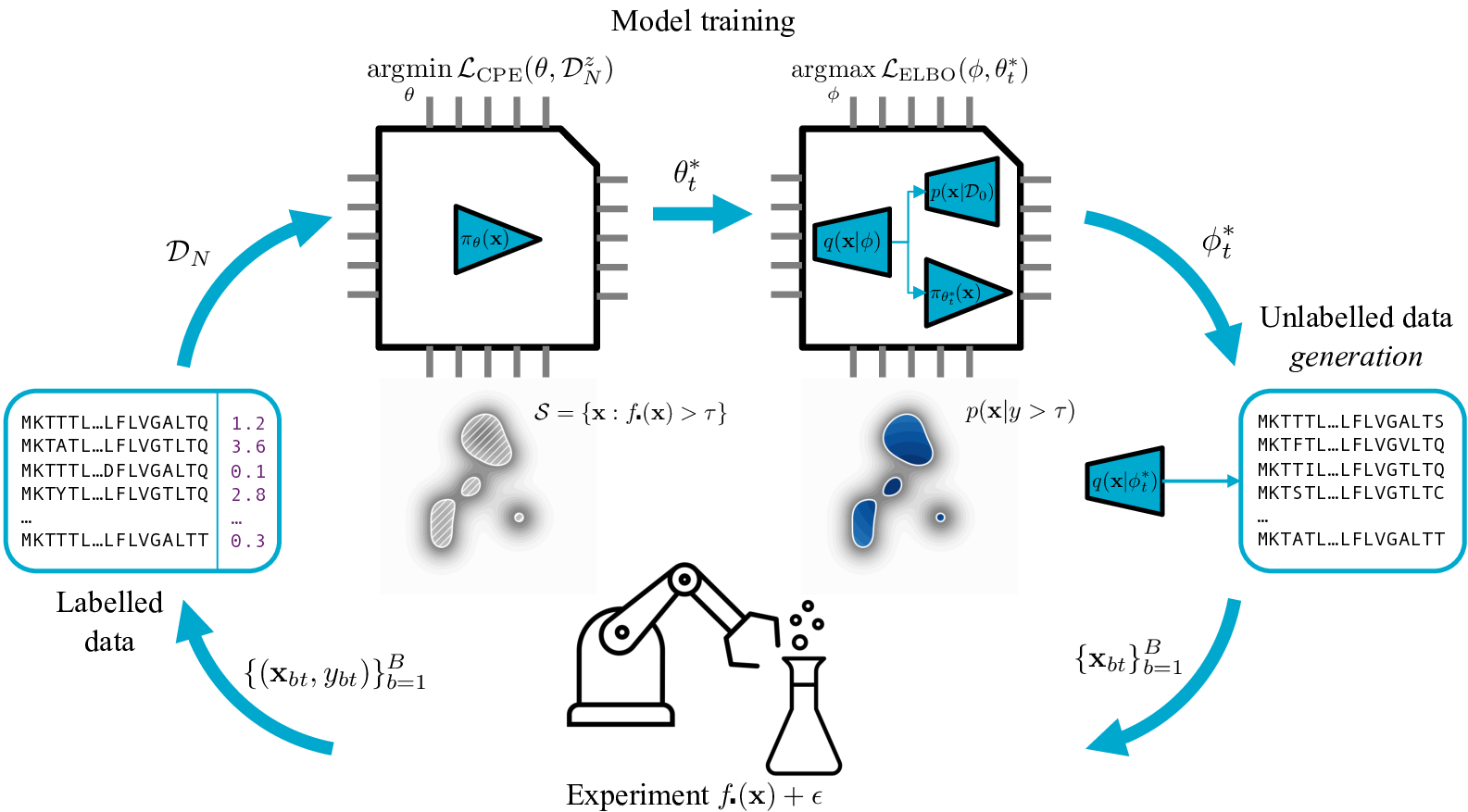
Active generation advances the union of generative modelling and black-box optimisation so that AI systems can design new artefacts — from molecules and materials to robotic components and algorithms — directly from high-level objectives. We combine powerful generative priors (transformers, flow matching etc.) with machine-learning optimisation loops that decide which experiments to run next, allowing the model to continually refine both its predictive beliefs and its search distribution. This fusion turns design problems that once relied on trial-and-error into targeted, data-driven discovery pipelines, yielding scalable tools for any domain where evaluating a candidate is expensive but generating hypotheses is cheap.
In Variational Search Distributions (VSD) we apply variational inference to the problem of active generation, and introduce a flexible framework for designing sequences such as proteins, with formal guarantees. Software for VSD can be found here. We extend this work for multi-objective optimisation problems in Amortized Active Generation of Pareto Sets, and then to reward model free settings in Generative Bayesian Optimization: Generative Models as Acquisition Functions. We have also applied these methods to actual protein engineering tasks.
We also investigate the spectral properties of sequence (protein, DNA) lansdcapes in Protein fitness landscape: spectral graph theory perspective. Using our theoretical framework we present propagational convolutional neural networks (PCNN), for which we derive theoretical guarantees on the generalization and convergence properties for protein property prediction.
Causal Inference - Machine learning as a tool for evidence-based policy
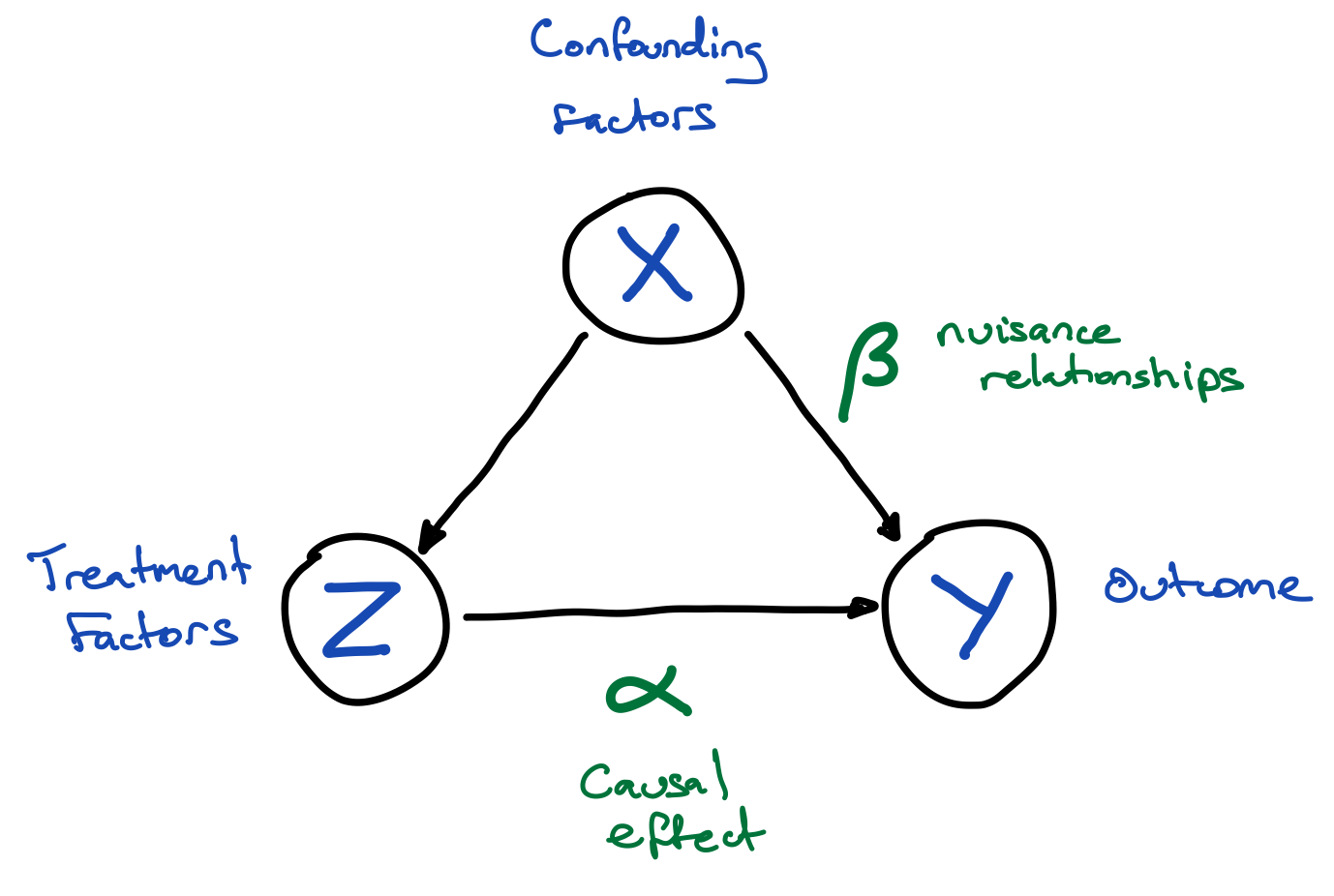
Machine learning (ML) can be a useful tool for observational causal inference studies, one of the cornerstones of evidence-based policy. ML can help us capture complex relationships in the data, thereby helping mitigate bias from model mis-specification. Also, use of regularisation in machine learning can lead to causal estimates with less error compared to unbiased methods when we have many related confounding factors in our data. I helped to write a blog post on this subject, and at Gradient Institute we have used machine learning for observational studies such as linking youth well-being to academic success. Reporting non-linear causal effects requires a new methodology, software for which we developed and can be found here.
Algorithmic Fairness - Fair Regression Algorithms
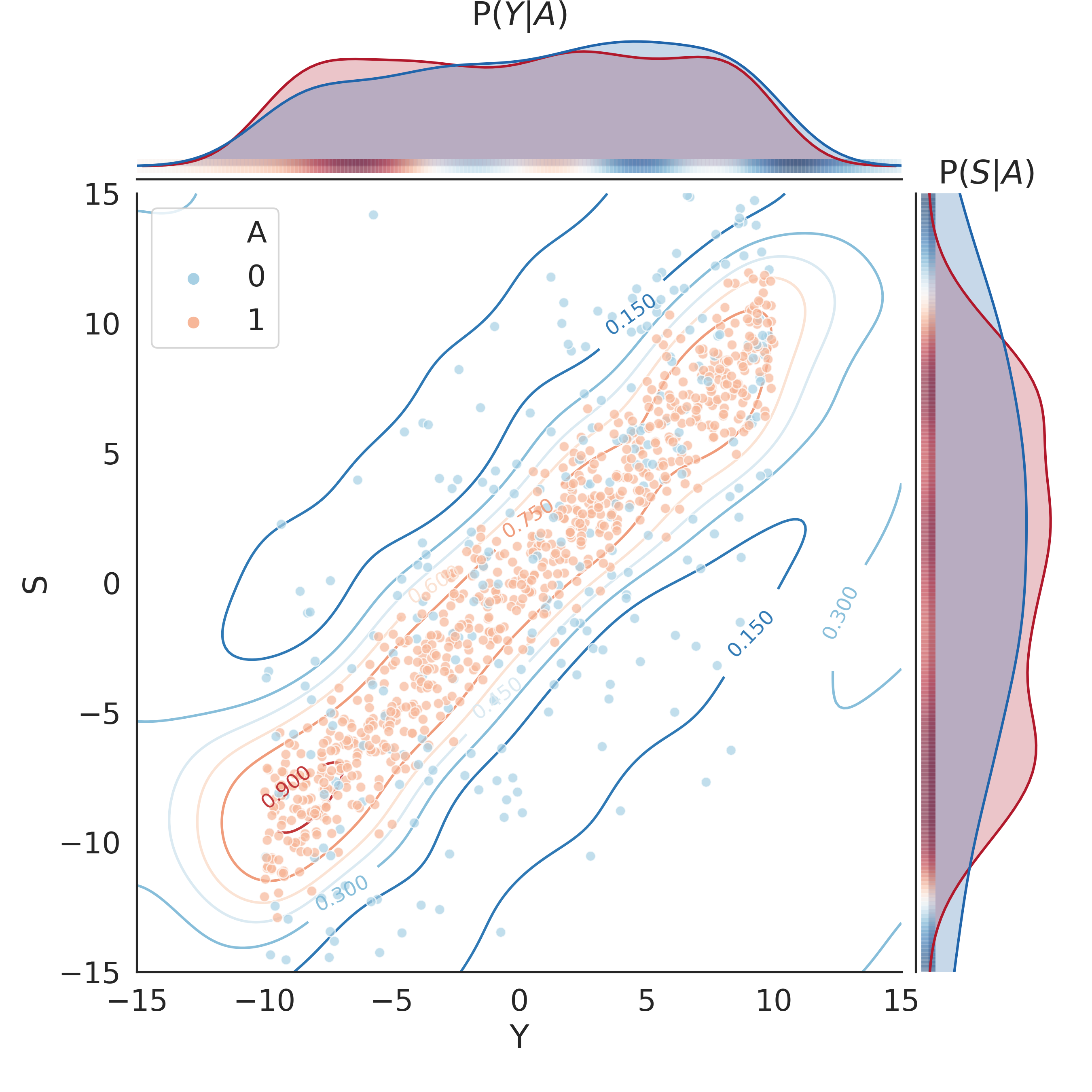
Algorithmic fairness involves expressing notions such as equity, equality, or reasonable treatment, as quantifiable measures that a machine learning algorithm can optimise. Mathematising these concepts, so they can be inferred from data is challenging, as is deciding on the balance between fairness and other objectives such as accuracy in a particular application. My research in this area along with others at the Gradient Institute has thus far focused on regression algorithms. Measuring the fairness of a regression algorithm is difficult compared to the classification case for many popular fairness criteria. Similarly, adjusting the predictions of a regressor is more complex than doing so for a classifier, and so our research has been targeting these areas. Here you can read more about measurement, and adjusting regression algorithms.
Landshark - Large-scale Spatial Inference with Tensorflow
Landshark is a set of python command line tools that for supervised learning problems on large spatial raster datasets. It solves problems in which the user has a set of target point measurements, such as geochemistry, soil classification, or depth to basement, and wants to relate those to a number of raster covariates, like satellite imagery or geophysics, to predict the targets on the raster grid.
Landshark fills a particular niche: where we want to efficiently learn models with very large numbers of training points and/or very large covariate images using TensorFlow. Landshark is particularly useful for the case when the training data itself will not fit in memory, and must be streamed to a minibatch stochastic gradient descent algorithm for model learning.
Please see the Landshark project page for more information.
Aboleth - A TensorFlow Framework for Bayesian Deep Learning
I am one of the primary creators of Aboleth, a bare-bones TensorFlow framework for Bayesian deep learning and Gaussian process approximation.
The purpose of Aboleth is to provide a set of high performance and light weight components for building Bayesian neural nets and approximate (deep) Gaussian process computational graphs. We aim for minimal abstraction over pure TensorFlow, so you can still assign parts of the computational graph to different hardware, use your own data feeds/queues, and manage your own sessions etc.
The project page is on github.
Revrand - Scalable Bayesian Generalised Linear Models


I am the project creator and primary contributor to revrand, a software library implements Bayesian linear models (Bayesian linear regression) and generalised linear models. A few features of this library are:
- A basis functions/feature composition framework for combining basis functions like radial basis functions, sigmoidal basis functions, polynomial basis functions etc.
- Basis functions that can be used to approximate Gaussian processes with shift invariant covariance functions (e.g. square exponential) when used with linear models.
- Non-Gaussian likelihoods with Bayesian generalised linear models using a modified version of the nonparametric variational inference algorithm with large scale learning using stochastic gradients (ADADELTA, Adam and others).
The project page is on github.
Extended and Unscented Kitchen Sinks
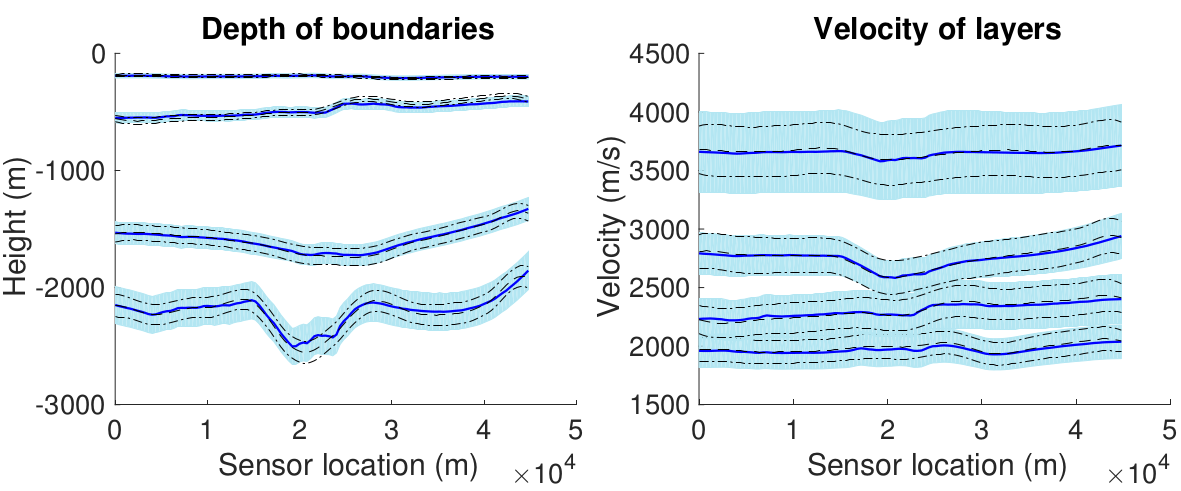
In this work we extended our Bayesian nonparametric algorithms for inverse problems, the unscented and extended Gaussian processes, to work with multiple outputs and over large datasets. The new algorithms are called unscented and extended kitchen sinks (EKS and UKS) since they use the random kitchen sink (or basis function) approximation for scaling kernel machines. This approximation allows us to straightforwardly enable the EKS and UKS to work in multiple output scenarios as well, enabling these algorithms to be useful for a wide variety of complex nonlinear inversion problems, such as geophysical inversions.
The impact of computerisation and automation on future employment
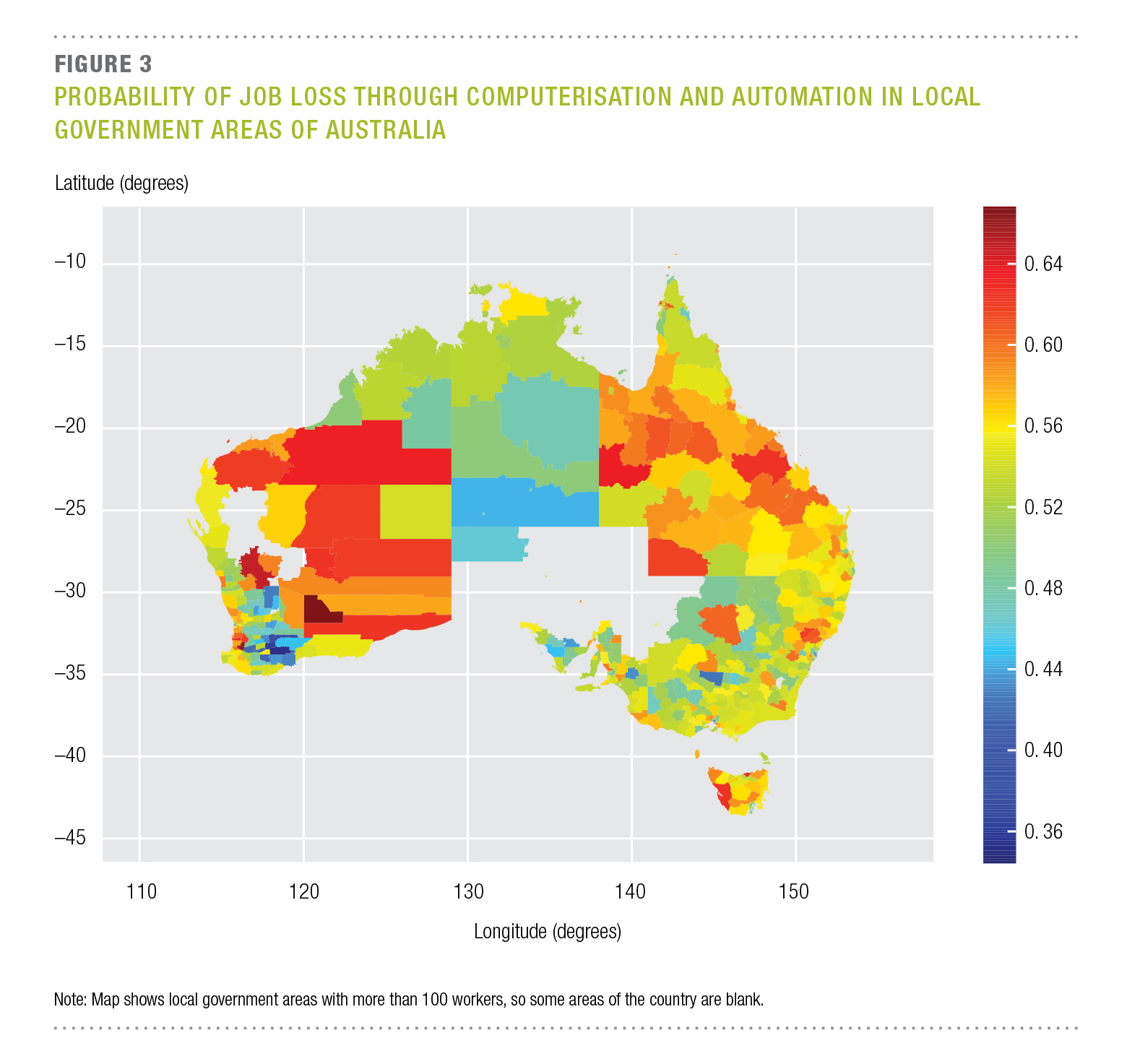
This work is a qualitative study into the susceptibility of jobs in Australia to computerisation and automation over the next 10 to 15 years. The methodology and initial data used is based on the much-cited paper by Frey and Osborne, which studied this same problem for the United States (US) and, more recently, for the United Kingdom (UK). The key to this work is trying to understand and quantify the impact of emerging technology on jobs and employment in areas such as artificial intelligence, robotics and machine learning.
The results show that 40 per cent of jobs in Australia have a high probability of being susceptible to computerisation and automation in the next 10 to 15 years. Jobs in administration and some services are particularly susceptible, as are regions that have historically associated with the mining industry. Jobs in the professions, in technical and creative industries, and in personal service areas (health for example) are least susceptible to automation. The report can be found here.
Nonparametric Bayesian Inverse Problems
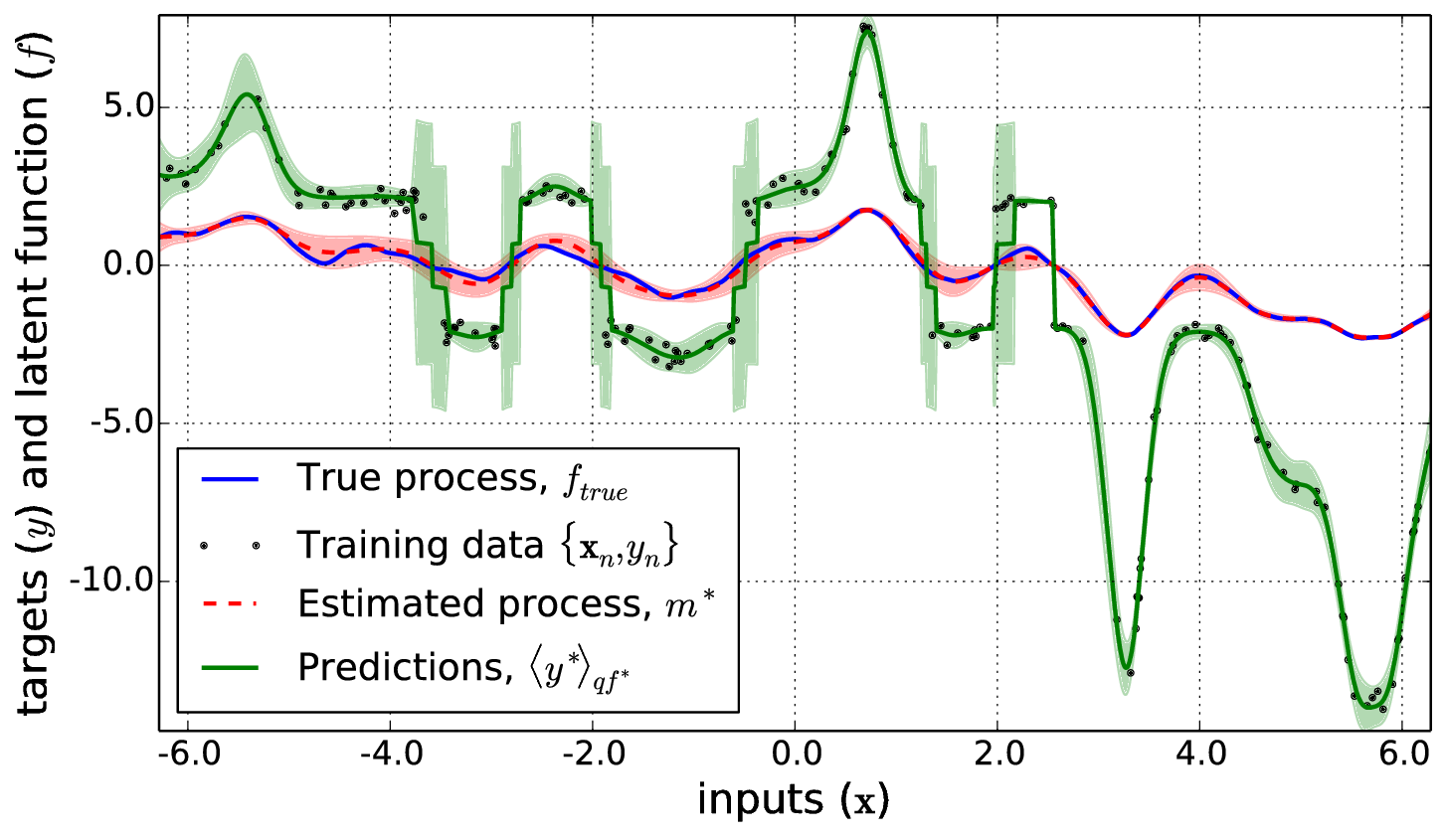
Nonlinear inversion problems, where we wish to infer the latent inputs to a system given observations of its output and the system’s forward-model, have a long history in the natural sciences, dynamical modeling and estimation. An example is the robot-arm inverse kinematics problem, where we wish to infer how to drive the robot’s joints (i.e. joint torques) in order to place the end-effector in a particular position, given we can measure its position and know the forward kinematics of the arm. Most of the existing algorithms either estimate the system inputs at a particular point in time like the Levenberg-Marquardt algorithm, or in a recursive manner such as the extended and unscented Kalman filters (EKF, UKF). In many inversion problems we have a continuous process; a smooth trajectory of a robot arm for example. Non-parametric regression techniques like Gaussian processes seem applicable, and have been used in linear inversion problems.
In this work we present two new methods for inference in Gaussian process (GP) models with general nonlinear likelihoods. Inference is based on a variational framework where a Gaussian posterior is assumed and the likelihood is linearized about the variational posterior mean using either a Taylor series expansion or statistical linearization. We show that the parameter updates obtained by these algorithms are equivalent to the state update equations in the iterative extended and unscented Kalman filters respectively, hence we refer to our algorithms as extended and unscented GPs. The unscented GP treats the likelihood as a ‘black-box’ by not requiring its derivative for inference, so it also applies to non-differentiable likelihood models. We evaluate the performance of our algorithms on a number of synthetic inversion problems and a binary classification dataset. See our NIPS spotlight paper for more details.
Unsupervised Scene “Understanding”


For very large scientific datasets with many image classes and objects, producing the ground-truth data for supervised (trained) algorithms can represent a substantial, and potentially expensive, human effort. In these situations there is scope for the use of unsupervised approaches, such as clustering, which can model collections of images and automatically summarise their content without human training.
To explore how modelling context effects clustering results, I derived several new algorithms that simultaneously cluster images and segments (super-pixels) within images. These algorithms also model collections of photos such as photo albums. Images are defined by whole-scene descriptors and the distribution of “objects” (segment clusters) within them. The images and segments are clustered using this joint representation, which is also more interpretable by people. The intuition behind this approach is that by knowing something about the type of scene (image cluster), object detection (segment clustering) can be improved. That is, we are likely to find trees in a forest. Additionally, by knowing about the distribution and co-occurrence of objects in an image, we have a better idea of the type of scene (cows and grass most likely make a rural scene).
These algorithms for unsupervised scene understanding outperform other unsupervised algorithms for segment and scene clustering. This is because of how they model context. These algorithms were even found to be competitive with state of the art supervised and semi-supervised approaches to scene understanding, as well as being scalable to larger datasets. See my ICCV paper, CVIU article and my thesis (ch. 5 & 6) for more information.
Clustering Images Over Many Datasets
Large image collections are frequently partitioned into distinct but related groups, such as photo albums from distinct environments that contain similar scenes. For example, a hiking holiday album may contain many images of forests and maybe a few villages. Whereas a conference trip album may have many urban scenes and images of people, with perhaps a few images of park-land. These groups, or albums, may be thought of as providing context for the images they contain.
I have formulated and applied a latent Dirichlet allocation-like algorithm to this problem. It shares image clusters between groups or albums, and keeps the proportion of clusters (mixture-weights) specific to each group, thereby modelling the context of the group. By doing this, the algorithm is actually better at finding clusters, and is often faster when dealing with large datasets, than regular mixture model based approaches. See my thesis (ch.4) for more information.
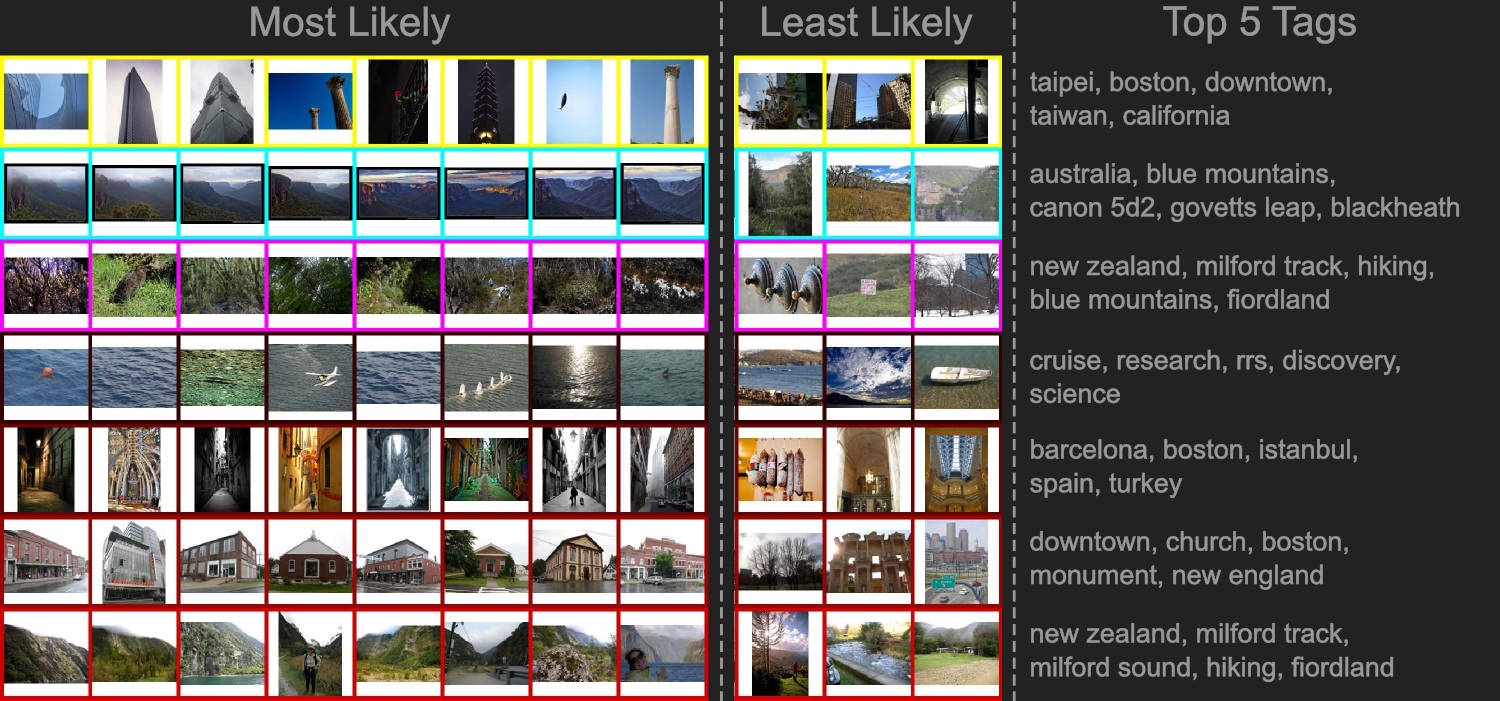
Clustering Images of the Seafloor
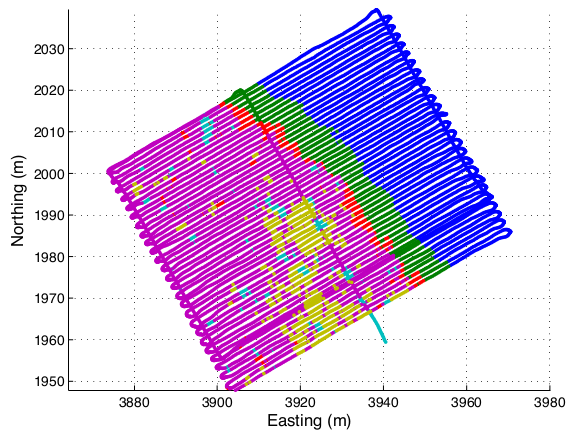
I have applied a Bayesian non-parametric algorithm, the variational Dirichlet process (with Gaussian clusters), to clustering large quantities of seafloor imagery (obtained from an autonomous underwater vehicle or AUV) in an unsupervised manner. The algorithm has the attractive property that it does not require knowledge of the number of clusters to be specified, which enables truly autonomous sensor data abstraction. The underlying image representation uses descriptors for colour, texture and 3D structure that are obtained from stereo cameras. This approach consistently produces easily recognisable clusters that approximately correspond to different habitat types. These clusters are useful in observing spatial patterns, focusing expert analysis on subsets of seafloor imagery, aiding mission planning, and potentially informing real time adaptive sampling. See my ISRR paper for more details.